INVERSE HANGING MEMBRANE: THE NATURTHEATER GRÖTZINGEN
Grötzingen, Germany
1977
Span: 42 m, Width: 28 m, Maximum Height: 10 m
Tessa Maurer, Elizabeth O'Grady, Ellen Tung
 |
| Figure 1 : A view of the Naturtheater Grötzingen from the stage. All five legs clearly support the 42-meter span shell, which covers approximately 900 seats. |
Social and Economical Context
The Naturtheater Grötzingen, shown in Figure 1, is an open-air outdoor theater located in Grötzingen, a small town near Karlsruhe, Germany. The theater is composed of a thin reinforced concrete shell that covers approximately 650 m2 of area and protects 900 audience members from rain and sunshine (see Figure 2) [1]. Architect Michael Balz and structural engineer Heinz Isler (1926 – 2009) designed the Naturtheater Grötzingen for a private community theater organization at Grötzingen [2]. In Germany, there is a law that only allows the construction of buildings with organic appearances in nature reserves. The suburb of Grötzingen is one such area, and therefore the structure needed to express a “natural” form and function well as an outdoor theater [3]. Figure 3 shows how well the theater is integrated with its natural surroundings.
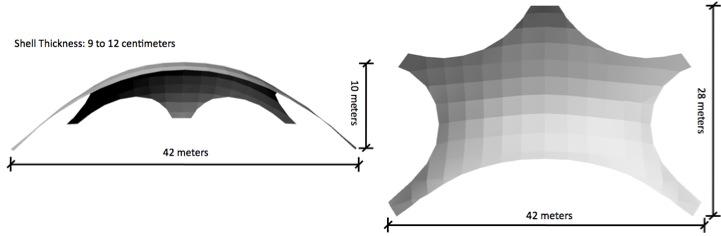 |
| Figure 2 : A diagram of the main dimensions of the Grötzingen Shell. The structure has an impressive span of 42 meters given its thickness of 9 to 12 centimeters. |
Heinz Isler strongly believes that the work of the architect and the engineer cannot be separated in shell design because of its inherent integration of aesthetics and statics [4]. Isler claims that if more than one person is involved in the design of a shell, “they must be willing to subordinate themselves to the emerging logic of the shell’s form as it evolves through experimentation” [5]. This ideal architect-engineer relationship is epitomized by the collaboration of Heinz Isler and Michael Balz, whose professional relationship started in 1967. Isler taught Balz various form-finding methods, and consequently the architect began to design his own creative shells by exploring hanging membranes and inflated forms [2]. Although Isler and Balz only worked on a few projects together in Germany, the resulting shells (including the Naturtheater Grötzingen, the Stetten Theater, and the Balz House) are some of the most elegant works that Isler produced in his career [6].
 |
| Figure 3 : Left: The legs of the shell flow freely into the ground, sometimes even appearing to be part of the ground. Right: From the back view, the shell appears to emerge like a natural piece of the landscape due to the change in elevation. |
Both Isler and Balz had always been interested in organic forms, which refers to shapes that are naturally derived from processes such as hanging, inflating, pouring and flowing. In particular, shell shapes have always served as a main source of inspiration in Isler’s work. The Swiss engineer was amazed that these naturally formed shells could be “wafer-thin and still resistant,” which led him to believe that the shell shape is always optimal [7]. Therefore, it is not surprising that the final form of the theater roof was a thin shell structure. Isler closely collaborated with Balz to find the ideal shape of the theater by using the method of inverting hanging membranes [2].
 |
| Figure 4 : Left: In his office, Balz explains the five-footed design using a plan drawing. Right: The view from inside the theater shows how the largest opening frames the stage, drawing the spectators’ eyes forward and creating a unique viewing experience. |
Besides its natural appearance, the design of the Grötzingen shell is particularly appropriate for an outdoor theater because of its acoustic effects and optimal sightlines. As shown in Figure 4, the structure contains five supports that are positioned strategically around the inclined seating area, opening the shell towards the theater stage with a maximum height of 10 meters. This shape favors speech acoustics from the stage while preventing excess sound reflection inside the shell [1]. Architects have criticized shells that are contained by planar windows because they believe that the “spatial flow” is interrupted by precise borders. However, for the Naturtheater Grötzingen, the absence of windows, the asymmetry of the form, and the clear opening towards the stage generate a spatial dynamic that encourages the exchange between interior and exterior [7]. This can be seen in Figure 5.
 |
| Figure 5 : The lack of defined boundaries allows for an integration of space between spectators and their surroundings. |
The dual-function of shells is advantageous since the roof, the space enclosure, and the load bearing supports are all achieved by one element. In particular, the Naturtheater Grötzingen is durable and waterproof without any surface coating because it is designed to be completely in compression (please refer to “Form Finding and Structural System”). However, the formwork for the theater during construction was quite expensive because it required laminated timber (glulam) beams that had to be manufactured specifically for the shape of the shell. The construction process was labor intensive and workers required special training by Isler himself. Nevertheless, the cost of the Naturtheater Grötzingen shell was still significantly cheaper than that of a tent construction of the same size [8].
Form Finding and Structural System
At the First Congress of the International Association for Shell Structures in Madrid, 1959, Isler presented a paper that outlined three new ways of finding shapes for shells. These methods were (1) The Freely Shaped Hill, (2) The Membrane Under Pressure, and (3) The Hanging Cloth Reversed [9]. The form of the Naturtheater Grötzingen was found with the third way, which Isler believes is the most efficient and accurate method since the loads acting on the hanging model and its reversed form are both gravitational forces.
When suspended under its own weight, a flexible chain forms a catenary curve that is subject to only tensile forces. When this curve is inverted, the form is subjected to only compression forces [10]. In the 1670s, British inventor, philosopher and architect Robert Hooke discovered that this catenary shape was the ideal form of an arch. In the late 1800s, Spanish architect Antonio Gaudí used this principle when he designed the crypt of the Church of Colònia Güell [10]. For his form-finding technique, the architect loaded hanging strings or chains with weights to create a series of intersecting curves. After he was satisfied with the form, Gaudí draped cloth around the model, took a picture, and turned the print upside down to use as the basis for his vaulted form [1].
 |
| Figure 6 : Balz explains the hanging membrane idea by showing example models for different projects. |
Isler’s form-finding method of the reversed hanging cloth was discovered serendipitously in the summer of 1955. On a building site he saw a piece of wet burlap draped over a mesh of steel bars. He noticed that within one square opening, the burlap hung in a domelike shape under its own weight. Isler concluded that the cloth carried itself in pure tension, so that when it was reversed it would become a form in pure compression [11]. The principle behind Isler’s hanging cloth method can be understood as the three-dimensional version of Hooke’s discovery; a piece of cloth that is hung from several fixed points will create an ideal form that is completely in tension. If the shape is “frozen” and flipped, the resulting shell should be in complete compression, which is convenient for concrete structures since concrete performs well in compression but poorly in tension. The main difference between the work of Gaudí and Isler is that the Spanish architect found his form through a network of two-dimensional catenary shapes while the Swiss engineer only used one hanging element (a piece of fabric) to determine the ideal form of his structure.
 |
| Figure 7 : The form on the left was made using cheesecloth cut at right angles to the supports, yielding a smooth hanging shape. In contrast, the form on the right was made using cheesecloth cut at a 45° angle to the supports, causing ridges between diagonal supports. |
Isler’s methods were completely based on physical modeling and experiments. In fact, he rarely used general mathematical theories when designing his shells [12]. To determine the form of the Naturtheater Grötzingen, Balz and Isler suspended fabric between supports that were displaced in the same relative positions as in the real structure, similar to the method shown in Figure 6. The support placements were particularly important to the Grötzingen project since the construction site had an inclined slope for audience seating. The orientation of the cut shape also affected the hanging form of the fabric. Figure 7 shows that if a shape is cut along the straight grain of the fabric, it hangs smoothly under its own weight; however, if the fabric is cut on a bias (a 45-degree angle), the shape of the hanging fabric forms natural ridges. Since the shell of the Naturtheater Grötzingen is completely smooth, one can infer that Isler and Balz used a membrane shape that was cut in the former orientation, not the latter (see Figure 8). The architect and engineer experimented with different forms by changing the support positions and varying the amount of material available for “sagging” and “edge overhangs” [2].
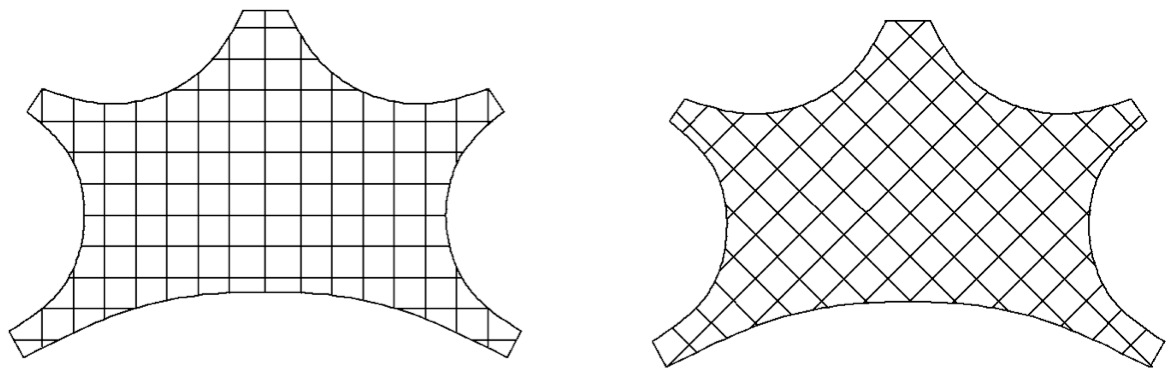 |
| Figure 8 : Left: The plan of the Grötzingen Shell aligned along the straight edge of the fabric, which would produce smooth hanging. Right: The shell plan aligned 45° to the straight edge fabric, which would produce unwanted ridges when hung. |
The final structural system of the Naturtheater Grötzingen is a reinforced concrete shell with the shell thickness varying from 9 cm to 12 cm [2]. Since the structure is in compression, buckling instability is an issue, particularly at the edges and supports of the shell. Isler does not use any stiffening edge beams in the Naturtheater Grötzingen; instead, he upturns the edges (which corresponds to the overhanging fabric in the hanging model) so that the double curvature required for increased stiffness is achieved without any increase in shell thickness [4]. However, to reduce the stresses in the supports, Isler simply tapered the legs so that they were thicker than the rest of the shell. The concrete shell weight is approximately 220 tons and the steel reinforcement is approximately 15 tons [8]. To prevent the shell from creeping outwards under its self-weight, the five supports are encircled and restrained by a steel foundation ring that takes the horizontal forces. Because the concrete is entirely in compression, the shell is impermeable and requires no surface coating to keep the structure waterproof. Furthermore, the inside of the shell is lined with echo-absorbing insulation panels that were left in from the formwork (please refer to “Construction”). These panels not only prevent excess echoing from the theater stage, but they also significantly reduce drumming sounds from the rain.
Structural Analysis
Isler had a profound aversion to computers and numerical analyses, believing that “theoretical considerations and derivations … are always based on severe simplifications of the assumptions.” Isler also stated that a further danger of numerical calculations lies in the fact that the computer can only answer the question asked and cannot identify questions that were not raised. The Swiss engineer therefore favored physical models to computational models. For very thin physical models, he used load testing to reveal both local and global instabilities of the structure [4]. The knowledge of each shell’s weak points allowed Isler to either revise his overall design or focus his reinforcement design in the weak areas. Although finite element analysis (FEA) was not fully developed until the 1970s, Isler refused to use computer-aided design when designing his later shells; in fact, the only computer in his office was used for word-processing [10]. He only conducted FEA on his structures to satisfy the authorities after the final form was already determined [13].
Although Isler used electronic strain gauges and buckling behavior load tests to determine the forces in his models, he was also confident that he could calculate stresses by hand within 15% of the actual stress in the shell. Isler’s form-finding method implies that bending moments are insignificant throughout most of the Naturtheater Grötzingen shell. When the form is hanging, the membrane is completely in tension and does not carry any moments. Therefore, the inverted form should not have any significant bending moments either. However, because Isler’s shells are in compression, buckling instability could be a problem for the Naturtheater Grötzingen roof. In fact, the buckling stability is the limiting factor for large thin shells, and Isler suggests that the maximum span for any shell should be limited to less than 90 meters [5].
Despite Isler’s aversion to computers, modern structural analysis programs can be used to understand the behavior of the Naturtheater Grötzingen. A simplified numerical model of the theater was created in SAP2000 (an FEA software), and a static dead-load analysis of the shell was run. Although Isler published his method for estimating stresses with hand calculations, he did not reveal the values of several important variables that were specific to the shape of the shell. Therefore, a comparison between the numerical model and Isler’s results are not feasible. Furthermore, several aspects of the SAP model are estimations and simplifications of the real shell, which can explain any unexpected results. The shell is represented as a series of quadrilateral elements rather than a continuous, smooth shell; the thickness is assumed to be a constant 10.5 centimeters (the average thickness) even though the thickness varies in the actual structure; the support conditions could only act at an element’s corner rather than along the entire length; and the analysis was run with SAP’s default values for normal-weight concrete only. While the analysis is not entirely realistic, it nevertheless produces reasonable explanations about the Grötzingen shell’s membrane forces and principal stresses.
While the Grötzingen shell is theoretically in complete compression, the results in the numerical model show some tension in the structure. This observation is probably due to the fact that the numerical model is approximated as a series of quadrilateral elements and SAP’s support conditions did not fully represent the actual supports in the real structure. The results of the analysis show that the maximum normal forces are 1152 kN/m in tension, and 2785 kN/m in compression. As shown in Figure 9, tension (positive values) is found in the legs and near the edges of the structure. In reality, the legs of the Naturtheater Grötzingen are thicker than the rest of the structure, and the edges of the structure are constructed with a stiffening double curvature. These aspects were not accounted for in the SAP model, and therefore the values of the membrane forces in the actual structureare likely to be smaller than what is shown. Nevertheless, the diagram in Figure 9 affirms Isler’s theory in that the structure is almost completely in compression.
 |
| Figure 9 : The normal force in the x-direction is found by averaging stress over the thickness of each element. The diagram shows that the Naturtheater Grötzingen is almost completely in compression. |
The principal stresses were also found for each element of the numerical model. Since the form of the Naturtheater Grötzingen was found from hanging a membrane, the shell should theoretically have no bending moments. However, the numerical analysis shows that the stresses in the top and bottom layers of the shell have different values, which means that there is bending present over the thickness of the shell (see Figure 10). This bending accounts for the slight tension observed in the shell, even though it is theoretically in complete compression.
The maximum principal stresses ranged from 15 MPa in tension to 14 MPa in compression. The minimum principal stresses ranged from 3 MPa in tension to 33 MPa in compression. While the values found in compression are reasonable for concrete, those found in tension are not. Concrete fails at around 2 MPa, which means that the extreme tension stresses are an order of magnitude too high for concrete alone. While this may be partly due to the numerical model’s inaccuracies and assumptions, it is still a high enough value to warrant concern. Besides thickening the legs and adding a double curvature to the shell edges, Isler also reinforced the Naturtheater Grötzingen with a steel wire mesh to resist tension. This reinforcement is even more important when considering the wind and snow loads, since these environmental factors can load the structure unevenly and create additional bending and tension in the shell.
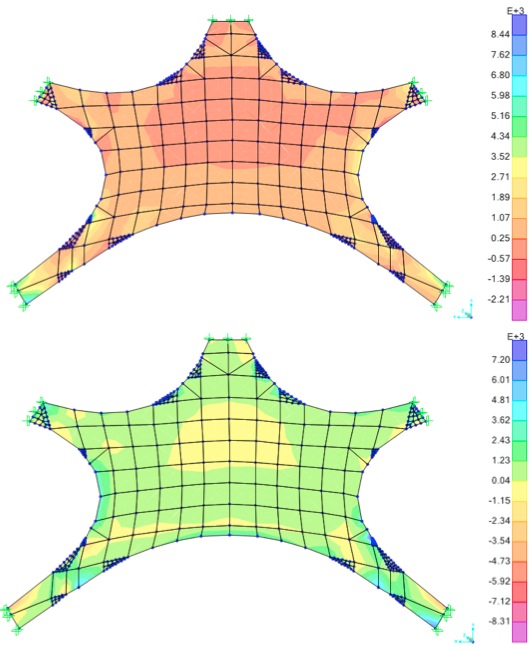 |
| Figure 10 : The different values of the maximum principal stresses in the top layer (top) and the bottom layer (bottom) of the shell show that there are bending moments present in the numerical model of the Naturtheater Grötzingen. |
In addition to analyzing the magnitudes of the principal stresses, the direction in which they act was evaluated in order to understand how the forces in the structure flow. The direction of the stress vectors indicate the flow of forces in the Naturtheater Grötzingen. The top image of Figure 11 shows the direction of the minimum and maximum principal stresses of each element in the form of arrows. While the length of the arrows gives some indication of the relative magnitude of the stresses, it is more accurate to consider magnitude based on the color of the arrows. The stress vectors indicate the flow of forces in the Naturtheater Grötzingen, demonstrating that forces generally move away from the center of the shell towards the five legs. A simplified model is also included to clearly show the flow of forces in the structure.
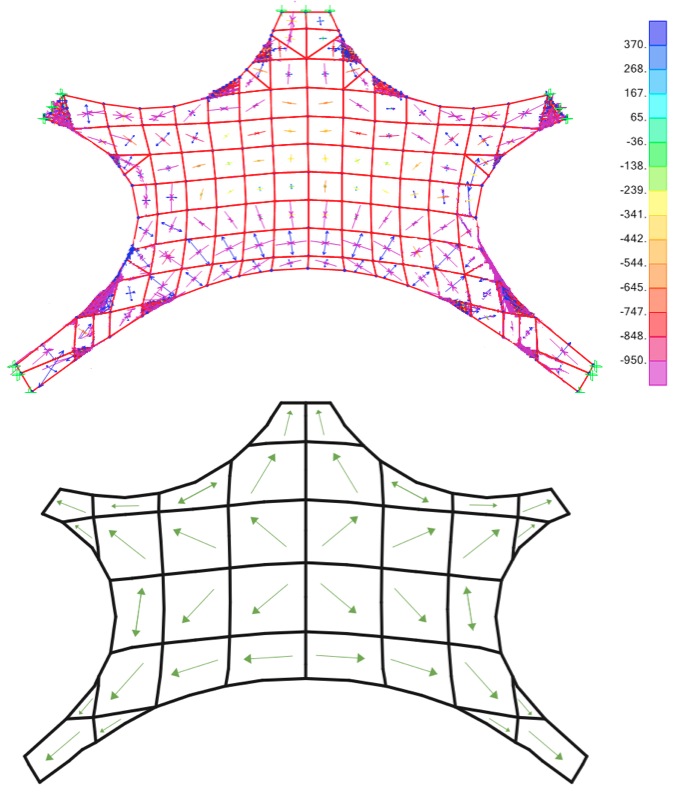 |
| Figure 11 : Top: The arrows on each element indicate the direction and magnitude of the maximum and minimum stresses. Bottom: The forces in the Naturtheater Grötzingen flow from the center of the shell, towards the legs, and into the supports. |
Construction
At the beginning of his career, Heinz Isler developed a specialized construction procedure for the shells he designed. Consequently, Isler had to convince a contractor to follow his ideas carefully and in 1955, Heinz Isler and Heinz Bösiger of the Bösiger Building Firm started an intensive and friendly cooperation that lasted for more than fifty years [12, 14]. Over this period of time, Isler personally trained all the construction personnel to specialize in his new building methods in shell construction. The Bösiger Building Firm built almost all of Heinz Isler’s shells in Switzerland, but Isler and Bösiger agreed to license other contractors for Isler’s work in France and Southern Germany, which included the Naturtheater Grötzingen project.
The construction of the Naturtheater Grötzingen was closely related to its design process. In particular, the formwork was a crucial step in the shell’s construction [4]. To determine the dimensions of the formwork, Isler and Balz took precise measurements on a grid of points across the surface of his physical model. They used a higher density of monitoring points in the “critical areas” that Isler had previously identified from load tests [10]. These measured dimensions were then scaled up so that formwork could be constructed accurately.
The formwork for each project was constructed of curved glue-laminated (glulam) timber beams that were cut specifically for the particular shell shape. Light scaffolding supported these timber beams, which then supported the cladding. For the Naturtheater Grötzingen, Isler and Balz chose to use wood-wool insulating panels with sound absorbing properties to clad the shell. This effectively prevented excess echoing in the structure, and today the slabs can be seen on the underside of the roof (see Figure 12). From his earlier shell-building experiences, Isler knew that approximately one out of ten thousand cladding panels fell after the formwork was removed. The German architect and the Swiss engineer did not want to take their chances for the Naturtheater Grötzingen, and therefore additional hooks were put in between the cladding and the concrete to ensure secure attachments [4].
 |
| Figure 12 : Left: The wood-wool insulating panels can be seen underneath the shell. Right: The wooden formwork for the shell construction left lasting, but subtle imprints in the hardened concrete. |
Although the Naturtheater Grötzingen shell theoretically does not require any reinforcement since it is in compression, Isler and Balz included two layers of steel reinforcement in the concrete to help the shell resist deformations, cracking, and non-uniform loads such as wind, snow, and earthquakes [4]. In fact, an earthquake occurred two years after the Naturtheater Grötzingen was completed but the shell was not damaged in any way [15]. Like the formwork, the concrete casting was also very important for the Grötzingen shell’s integrity. The concrete mixture had to be uniform, workable, yet stiff enough so that the concrete could be cast on inclined surfaces. Therefore, plasticizers were used to create workable concrete, and retarders were added to the mixtures to prevent the concrete from hardening too quickly. The Grötzingen shell was poured in one step to ensure uniformity and adequate bonding between different batches of concrete. Furthermore, Balz and Isler understood that the building environment also affects the structural behavior of concrete. Consequently, the contractors were required to cast the Naturtheater Grötzingen on a clear, warm day since casting in rain would wash away the new concrete and casting in temperatures under four degrees Celsius would cause the concrete to set too quickly. Finally, the construction workers had to trowel the concrete carefully to eliminate porosity. This required a lot of physical agility since the workers had to trowel on top of the shell without touching any finished sections [4].
Conclusion
Many people today consider Heinz Isler as one of the greatest structural artists in the twentieth century. His attention to aesthetics and his love for nature are evident in all his thin shell structures. Furthermore, Isler’s revolutionary form-finding techniques and his unique construction methods clearly set him apart from other noteworthy structural engineers. His projects are efficient (they use minimum materials), economical (they are competitive with other structural systems) and elegant in design. Isler’s collaboration with Balz was an extremely successful partnership because Isler taught Balz his methods of form-finding and the architect was consequently able to develop elegant, organic designs for their projects in Southern Germany. Their professional relationship was the epitome of Isler’s definition of the ideal cooperation between engineers and architects in shell design.
Isler and Balz believed that complicated mathematical techniques were not the right way to analyze the Naturtheater Grötzingen because of its naturally found form. Instead, Isler measured the stresses in his models with electronic strain gauges and monitored deflections in his shells years after their construction. He found that the maximum deflection to span length was very small in most of his shells. In fact, the Naturtheater Grötzingen is one of the best performing shells with a deflection to span length ratio of only 1/4000 [11]. Today, the Naturtheater is still in use by the same Grötzingen community theater group that commissioned the project. The venue frequently hosts performances of popular plays and invites international theater groups to use the space, allowing people from all over the world to enjoy the elegance and durability of the Grötzingen shell.
 |
| We would like to thank Michael Balz who shared his time, expertise, and experience with us. |
1. Chilton, John C. Heinz Isler: The Engineer’s Contribution to Contemporary Architecture. London: Thomas Telford, 2000.
2. Interview with Michael Balz (October 28 2012).
3. Balz, Michael. “Working with Heinz Isler.” Journal of the International Association for Shell and Spatial Structures, no.169 (2011): 155-160.
4. Isler, Heinz. “Concrete Shells Derived from Experimental Shapes.” Structural Engineering International, no.4 (1994): 142-147.
5. Isler, Heinz. “New Shapes for Shells.” Bulletin of the International Association for Shell Structures, no.8 (1960): Paper C-3.
6. Abel, John & John Chilton. “Heinz Isler – 50 Years of “New Shapes for Shells”: Preface.” Journal of the International Association for Shell and Spatial Structures, no.169 (2011): 131-134.
7. Kotnik, Toni & Joseph Schwartz. “The Architecture of Heinz Isler.” Journal of the International Association for Shell and Spatial Structures, no.169 (2011): 185-190.
8. Michael Balz’s Website. www.michael-balz.de/kap3a_4.htm (accessed November 14 2012).
9. Billington, David P. The Tower and the Bridge: The New Art of Structural Engineering. New York: Basic Books, 1983.
10. Chilton, John C. “Heinz Isler’s Infinite Spectrum: Form Finding in Design.” Architectural Design, no.80 (2010): 64-71.
11. Billington, David P. & Jameson W. Doig. The Art of Structural Design: A Swiss Legacy. USA: Yale University Press, 2003.
12. Garlock, Maria E. Moreyra & David P. Billington, Sr. Félix Candela: Engineer, Builder, Structural Artist. USA: Yale University Press, 2008.
13. Ramm, Ekkehard. “Heinz Isler Shells – The Priority of Form.” Journal of the International Association for Shell and Spatial Structures, no.169 (2011): 143-154.
14. Bösiger, Heinz. “The Building of Isler Shells.” Journal of the International Association for Shell and Spatial Structures, no.169 (2011): 161-169.
15. Balz, Michael. “Working with Heinz Isler.” Journal of the International Association for Shell and Spatial Structures, no.169 (2011): 155-160.






